
FACULTY OF EXACT AND NATURAL SCIENCES
TWENTY YEARS OF JOINT RESEARCH
Natural forms affect all of us, not only for their beauty but also for their diversity. It is still not known whether forms define the essence of the phenomena associated with them, or vice versa--that forms are natural consequences of the phenomena.
Since ancient times, scientists have tried different methods to study forms and their properties. In mathematics, the study of form has often used geometric approaches. Over time research has led researchers in beautiful as well as interesting and challenging directions. Plato and his school emphasized the study of pure geometric shapes (νοηtά – mental) and their properties, while Archimedes, Apollonius of Perga, Euclid, Heron and their followers used geometric methods to explain phenomena (αiσθητα – Observable, classification of Geminus of Rhode I B.C).
In the early 17th century an inevitable conclusion of the study of Kepler and Galilei was that the trajectory of objects was directly related to the study of conic sections (second order plane lines). This insight has been further strengthened with Newton’s law of gravitation. Although Newton's approach was originally geometric, mechanics and other natural sciences have developed rapidly and over time mathematicians have used different approaches, including calculus, algebra and others. This process permitted René Descartes and Pierre de Fermat to create the foundations of analytical geometry and more expanded applied methods in geometry. This permitted mathematicians to calculate the form of objects and the trajectory of their motions using analytical formulas.

Although a complete overview is impossible in one article, we have chosen two approaches that have been developed almost simultaneously since 1994 by two different teams—one by a Belgian group and the other by a Georgian-Italian team. In 1994, the Belgian scientist Johan Gielis became interested in the possibility of the analytical representation of the forms of plants. He continued in the footsteps of the French mathematician, Gabriel Lamé, and wrote the so-called „superformula“ now known as the Gielis Superformula.
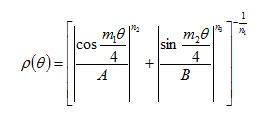
When (m1=m2=4, A=B=1 and n1=n2= n3=n) the Superformula represents Lamé2s curves.
There was a very interesting and unexpected occurrence. Using a specific selection of parameters for the Superformula, the team discovered that it describes the forms of many organisms. A beautiful book was devoted to these issues and published in Belgium in 2003 (Johan Gielis - Inventing the Circle: The Geometry of Nature). This scientific approach became very popular and the formula was adopted by many mathematicians, including Tom Gerats (Netherlands), Yohan Fougerolle (France), Pierpaolo Natalini (Italy) and others.
The Georgian-Italian group was founded by two professors, Paolo Ricci and Ilia Tavkhelidze, who have worked since 1998 on how the solution of the boundary-value problem for the partial differential equation depends on the geometrical structure of domain. The natural extension of the problems had been formulated in various forms by the teachers of these scientists, Ilia Vekua, Gaetano Fichera and Olga Oleinik. It is very important to have an analytical representation of the geometry of the domain in order to carry out fundamental work on these problems. After using the theories of the outstanding French scientist Gaspard Monge (teacher of Gabriel Lamé) for several years, and starting from and developing out of the ideology of the local toroidal coordinates, it became possible to create an analytical representation of a wide class of geometric shapes and surfaces. Today, this domain is referred to as GRT (Generalized Revolving and Twisting) figures or, sometimes as Surfaces of Revolution. These figures are mathematically represented as follows:
The authors represent objects using the geometric essence of five different functions and two parameters (i.e. what process each of them defines). With this presentation, it was possible to describe the Generalized Möbius-ListingTs bodies and surfaces and to study the unique and interesting properties of these objects. A final paper on these investigations was published as “The Classification of a Wide Set of Geometric Figures, Surfaces and Trajectories” in Rendiconti Academia Nazionale delle Scienze detta dei XL, Memorie di Matematica e Applicazioni, Serie V, vol.XXX, Parte 1, 2006 - 124 o, Dalla Fondazione (1782) Roma, pp. 191-212 by I.Tavkhelidze and P.E. Ricci,.
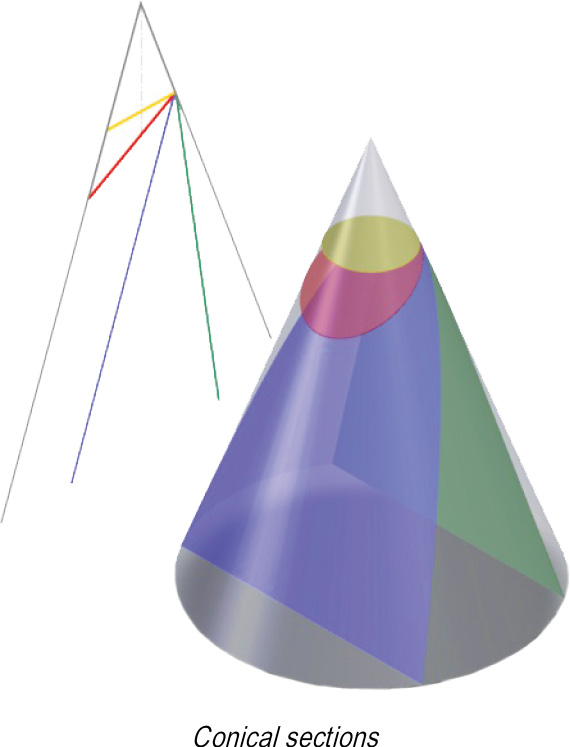 Of particular interest was part of I. Tavhelidze’s work based on the formula/ representation (2), in which he studied the scuttingc of Generalized Möbius-Listing s surfaces. Since 2007, these results have been presented at several international conferences and were specially mentioned at the Ukrainian Mathematical Congress in 2009 (Kiev, Ukraine).
Of particular interest was part of I. Tavhelidze’s work based on the formula/ representation (2), in which he studied the scuttingc of Generalized Möbius-Listing s surfaces. Since 2007, these results have been presented at several international conferences and were specially mentioned at the Ukrainian Mathematical Congress in 2009 (Kiev, Ukraine).
The group has further expanded to work jointly with other Italian colleagues such as Caterina Cassisa, Diego Caratelli and Sergio Camiz. The practical significance and new perspectives of this new collaboration attracted the Georgian physician, Professor Mamanti Rogava, who posed a new set of challenges to his colleagues: Whether they can record the complex motion of a complex geometric object’s analytical formula. He identified one of the most important applied fields for the application of the study of forms-- the dynamics of human organs.
The year 2010 was a turning point for both groups – Paolo Ricci, Diego Caratelli and Johan Gielis met at an international conference and introduced other members of the groups to each other via Internet. They had a common task, but their approaches were different. After presenting the methods, Ilia Tavkhelidze proposed the idea of using Johan Gielis’ representation twice in the representation formula written by his group. Consequently, the Gielis shape started “to rotate” around the Gielis curve. In turn, a Belgian-Dutch-French group showed interest in cutting generalized Mobius Listing bodies and launched joint research that is still intensively underway.
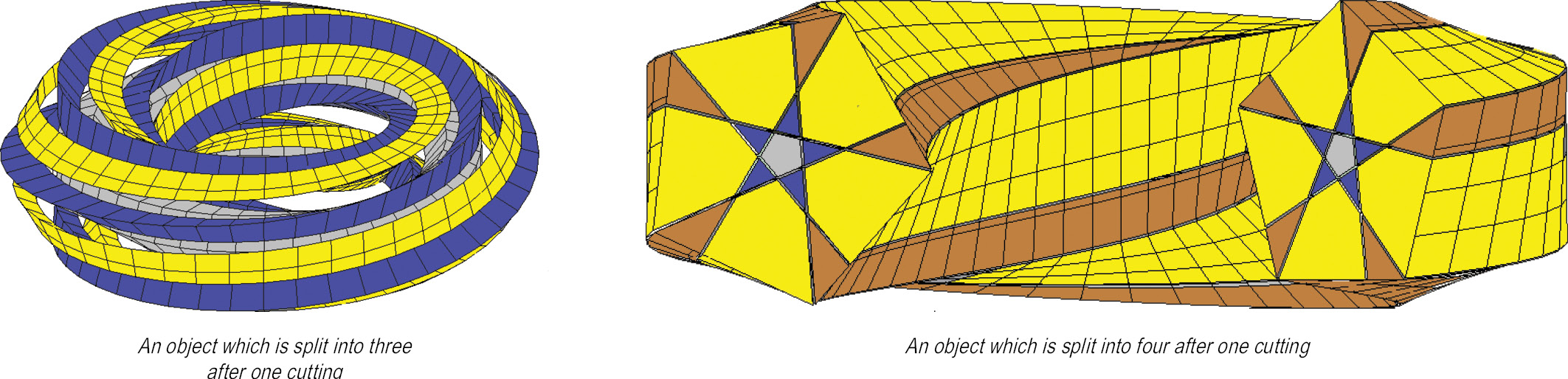
The essence of one “unexpected” phenomenon is as follows: Usually after one cutting, an object is split into two parts. The “Mobius strip” is a well-known exception, however, which still remains whole after cutting. It became evident that three-dimensional Mobius Listing bodies could yield more than two objects with only a single cutting. These are not mere teoretical results, as real-life examples demonstrated. Studying the shape, structure, twists and other properties of these objects proved an extremely important problem, not only from a mathematical point of view, but also for their application in studying mathematical models like the structure of plants, cell formation, animal dynamics and complex molecular chemical structures. The geometrical figures studied proved to be very interesting from an aesthetic point of view, and during the summit ‘Mathematics and Art’ organized by the Royal Flemish Academy of Belgium in 2012, the report prepared by the group created a significant interest In 2013 this work was published by the Lincei Academy (“About ‘Bulky’ Links, Generated by Generalized Mëbius-Listing’s bodies GMLn3 ”, I. Tavkhelidze, C.Cassisa, J.Gielis and P.E.Ricci, Rendiconti Lincei Mat. Appl. 24 (2013), pp. 11-38).
 The members of the Georgian-Italian group joined the process of understanding the problem put forward by their colleagues – whether shapes existing in nature are somehow strictly determined by their functionality and purpose, or are determined by forces of nature acting in the past. For example, is the shape of a flower pre-determined by its future purpose, or is it shpaed by natural foces and elements, such as wind, gravity and ambient temperature. Joint work was undertaken as a result of very intensive activities by Johan Gielis, Diego Caratelli, Yohan Fougerolle, Paolo Emilio Ricci, Ilia Tavkhelidze and Tom Gerats. This resulted in the publication of “Universal Natural Shapes: From Unifying Shape Description to Simple Methods for Shape Analysis and Boundary Value Problems", in journal PlosONE , 27,IX, 2012, pp.1-18. This article unites the opinions of scientists from a number of universities, such as the University of Antwerp (Belgium), Delft University of Technology (Netherlands), the University of Burgundy (France), Campus Bio-Medico University (Italy) and Tbilisi State University. Later in 2012 several professors from the Universities of Salerno (Italy), Vilnius (Lithuania) and Baku (Azerbaijan) also joined the activity.
The members of the Georgian-Italian group joined the process of understanding the problem put forward by their colleagues – whether shapes existing in nature are somehow strictly determined by their functionality and purpose, or are determined by forces of nature acting in the past. For example, is the shape of a flower pre-determined by its future purpose, or is it shpaed by natural foces and elements, such as wind, gravity and ambient temperature. Joint work was undertaken as a result of very intensive activities by Johan Gielis, Diego Caratelli, Yohan Fougerolle, Paolo Emilio Ricci, Ilia Tavkhelidze and Tom Gerats. This resulted in the publication of “Universal Natural Shapes: From Unifying Shape Description to Simple Methods for Shape Analysis and Boundary Value Problems", in journal PlosONE , 27,IX, 2012, pp.1-18. This article unites the opinions of scientists from a number of universities, such as the University of Antwerp (Belgium), Delft University of Technology (Netherlands), the University of Burgundy (France), Campus Bio-Medico University (Italy) and Tbilisi State University. Later in 2012 several professors from the Universities of Salerno (Italy), Vilnius (Lithuania) and Baku (Azerbaijan) also joined the activity.
During the same period, an analytical representation of “difficult” movements of shapes was developed at the Tbilisi State University which later laid the foundation for receiving new results from a mathematical point of view.
Using the given formulas, it is possible to provide non-trivial geometrical figures and their movements by selecting seven functions (T(t)º(T1(t), T2(t), T3(t)), R(q,t), p(t,y,q,t), g(t), n(q), M(t), K(q,t)) from a geometrical point of view, and to split difficult movements into “elementary movements.”
The results obtained by the joint international and interdisciplinary group are an important precondition for the modern understanding of certain tasks that arise in fields such as the practice of medicine, in biology, in nanotechnology, and determining antenna patterns, etc. Joint activity with Professor Vilija Targamadze from the University of Vilnius has revealed the use of this trend in problem-based learning (PBL), by taking into consideration the complexity of the issue, its originality and “endlessness”.
 These approaches paved the way for an active involvement by computer technologies in the process of understanding the most difficult practical and theoretical issues through mathematical modeling. Quite different approaches by Yohan Fougerolle from the University of Burgundy, and Levan Roinishvili from St. Andrew, the First-Called Georgian University of the Patriarchate of Georgia, are noteworthy. This team group received a proposal from Springer Publishing to publish their scientific work as a book. At the initiative of the Belgian team, the Institute of Geometry at the Antwerp Institute of Geometry will finance a PhD program in geometry for three PhD students at TSU, as well as a program on mathematics for computer science with the Italian partners, and a part of the program on computer modeling with the French collaborators.
These approaches paved the way for an active involvement by computer technologies in the process of understanding the most difficult practical and theoretical issues through mathematical modeling. Quite different approaches by Yohan Fougerolle from the University of Burgundy, and Levan Roinishvili from St. Andrew, the First-Called Georgian University of the Patriarchate of Georgia, are noteworthy. This team group received a proposal from Springer Publishing to publish their scientific work as a book. At the initiative of the Belgian team, the Institute of Geometry at the Antwerp Institute of Geometry will finance a PhD program in geometry for three PhD students at TSU, as well as a program on mathematics for computer science with the Italian partners, and a part of the program on computer modeling with the French collaborators.
The results received by a joint international and interdisciplinary group are an important precondition for new understanding of certain tasks raised in practice in the fields of medicine, biology, nanotechnology, antenna design, etc.




